Your First Circuit

Let's build your first digital circuit with SHDL!

What We're Building

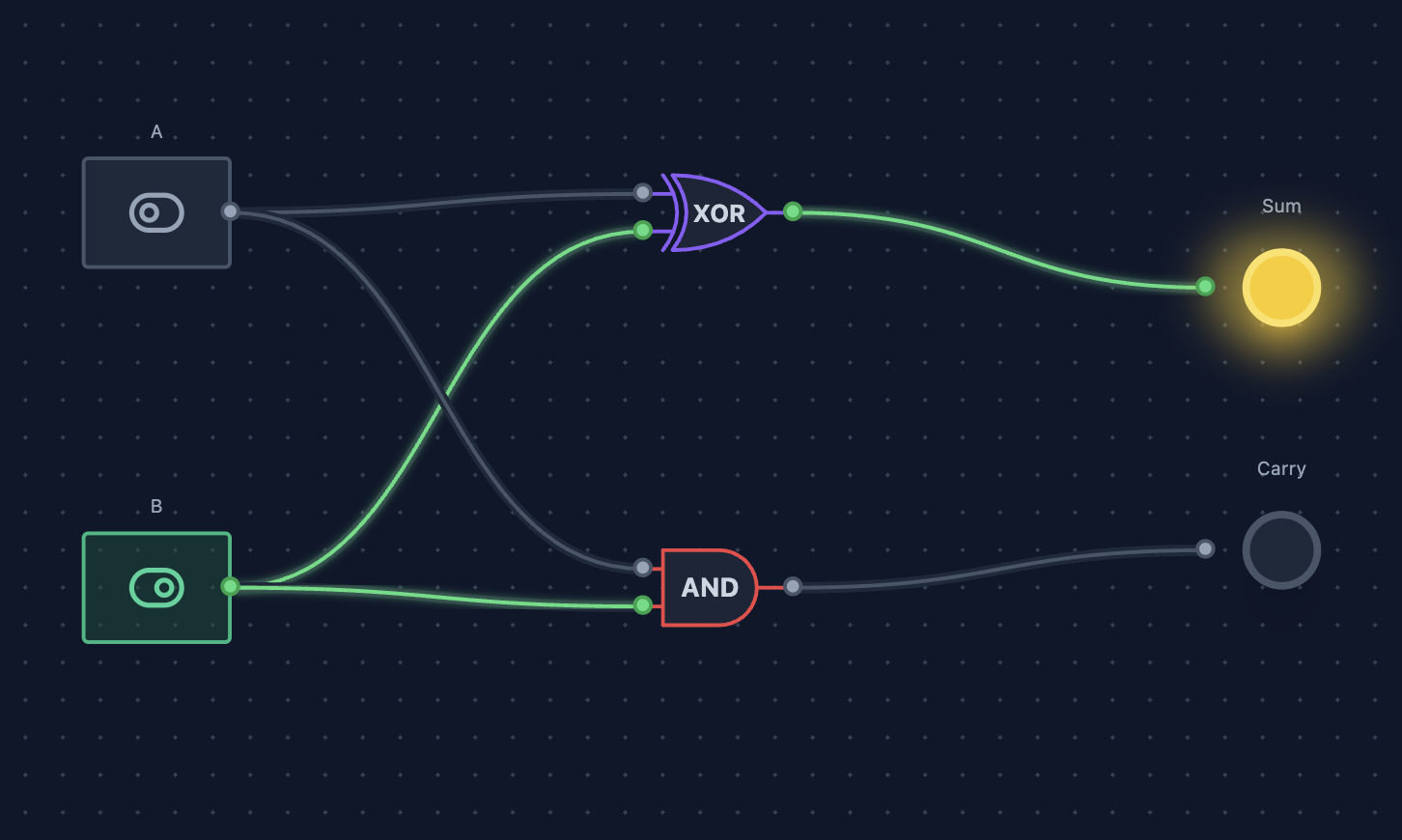
We'll create a half adder - a fundamental building block in digital arithmetic. A half adder takes two single-bit inputs and produces a sum and a carry output.

A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Create the File

Create a new file called halfAdder.shdl:

component HalfAdder(A, B) -> (Sum, Carry) {
    xor1: XOR;
    and1: AND;
    
    connect {
        A -> xor1.A;
        B -> xor1.B;
        A -> and1.A;
        B -> and1.B;
        xor1.O -> Sum;
        and1.O -> Carry;
    }
}

Understanding the Code

Let's break down each part:

Component Declaration

component HalfAdder(A, B) -> (Sum, Carry) {

• component - keyword to define a new component
• HalfAdder - the name of our component
• (A, B) - input ports
• -> (Sum, Carry) - output ports

Instance Declarations

xor1: XOR;
and1: AND;

These create instances of primitive gates:

• xor1 - an XOR gate
• and1 - an AND gate

Connect Block

connect {
    A -> xor1.A;
    B -> xor1.B;
    ...
}

The connect block defines how signals flow:

• A -> xor1.A means "connect input A to the A port of xor1"
• Signals flow from left (source) to right (destination)

Compile the Circuit

Use PySHDL's command-line tool to compile your circuit:

shdlc compile halfAdder.shdl

This will generate C code that can be used for simulation.

Simulate with Python

The PySHDL library provides a wrapper for you to interact with your circuits directly in Python:

from pyshdl import Circuit

with Circuit("halfAdder.shdl") as circuit:
    # Test all input combinations
    for a in [0, 1]:
        for b in [0, 1]:
            circuit["A"] = a
            circuit["B"] = b
            circuit.step()
            print(f"A={a}, B={b} -> Sum={circuit['Sum']}, Carry={circuit['Carry']}")

Output:

A=0, B=0 -> Sum=0, Carry=0
A=0, B=1 -> Sum=1, Carry=0
A=1, B=0 -> Sum=1, Carry=0
A=1, B=1 -> Sum=0, Carry=1

Visualize the Circuit

You can think of the half adder like this:

Next Steps

Now that you've built a half adder, try:

1. Building a full adder using two half adders
2. Chaining full adders to make an 8-bit adder
3. Exploring the Language Reference for more features

See the Examples section for more complex circuits!